

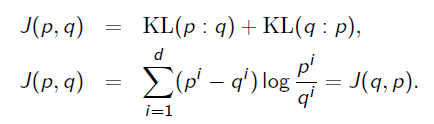

Once we get a centroid, you can use center-based clustering techniques like k-means (Lloyd batched updates or Hartigan single swap update). Note that the center relocation in k-means need not be the optimal centroid but only improves over the current center: This is called variational k-means and applies to the Jeffreys frequency approximation technique.

|

|
| Barbara | Lena |
3.8109756E-6 3.8109756E-6 3.8109756E-6 4.5731707E-5 2.5152438E-4 4.2682927E-4 6.2881096E-4 9.984756E-4 0.0011775915 0.0016463414 0.0020503048 0.0026028964 0.0032278963 ...
setwd("C:/testR")
We load the histograms as follows:
lenah=read.table("Lena.histogram")
barbarah=read.table("Barbara.histogram")
You can print the histogram of lena simply by typing in the R console:
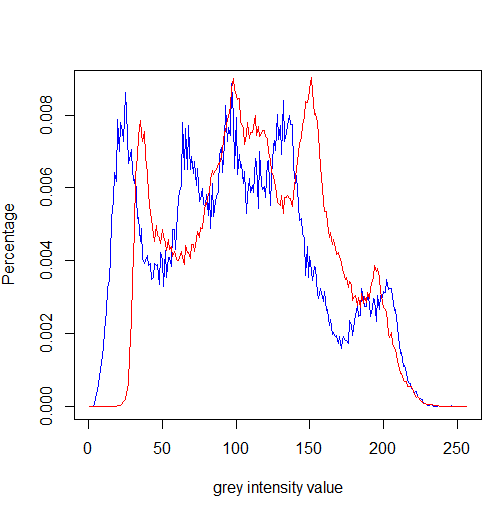
lenahLet us visualize the frequency histograms:
plot(lenah[,1], type="l", col = "blue", xlab="grey intensity value", ylab="Percentage") lines(barbara[,1], type="l",col = "red" )
source("JeffreysSKLCentroid.R")
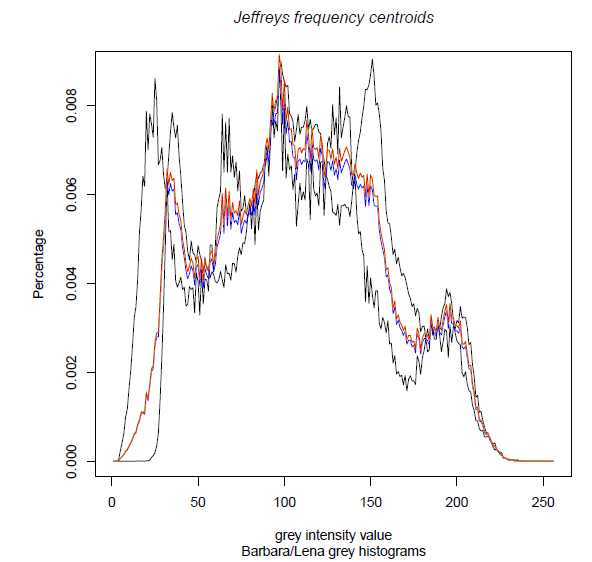
To compute the following centroids:
n<-2 d<-256 weight=c(0.5,0.5) set<- array(0, dim=c(n,d)) set[1,]=lenah[,1] set[2,]=barbarah[,1] approxP=JeffreysPositiveCentroid(set,weight) approxF=JeffreysFrequencyCentroidApproximation(set,weight) approxFG=JeffreysFrequencyCentroid(set,weight)We can now visualize the three centroids:
pdf(file="SKLJeffreys-BarbaraLena.pdf", paper ="A4") typedraw="l" plot(set[1,], type=typedraw, col = "black", xlab="grey intensity value", ylab="Percentage") lines(set[2,], type=typedraw,col = "black" ) lines(approxP,type=typedraw, col="blue") # green not visible, almost coincide with red lines(approxF, type=typedraw,col = "green") lines(approxFG,type=typedraw, col="red") title(main="Jeffreys frequency centroids", sub="Barbara/Lena grey histograms" , col.main="black", font.main=3) dev.off() graphics.off()
randomUnitHistogram<-function(d)
{
result=runif(d,0,1);
result=result/(cumsum(result)[d])
result
}
n<-10 # number of frequency histograms
d<-25 # number of bins
set<- array(0, dim=c(n,d))
weight<-runif(n,0,1);
cumulw<-cumsum(weight)[n]
# Draw a random set of frequency histograms
for (i in 1:n)
{set[i,]=randomUnitHistogram(d)
weight[i]=weight[i]/cumulw;
}
A=ArithmeticCenter(set,weight)
G=GeometricCenter(set,weight)
nA=normalizeHistogram(A) # already normalized
nG=normalizeHistogram(G)
# Simple approximation (half of normalized geometric and arithmetic mean)
nApproxAG=0.5*(nA+nG)
optimalP=JeffreysPositiveCentroid(set,weight)
approxF=JeffreysFrequencyCentroidApproximation(set,weight)
# guaranteed approximation factor
AFapprox=1/cumulativeSum(optimalP);
# up to machine precision
approxFG=JeffreysFrequencyCentroid(set,weight)
Finally, let us output graphically those centroids into a pdf file:
pdf(file="SKLJeffreys-ManyHistograms.pdf", paper ="A4")
typedraw="l"
plot(set[1,], type=typedraw, col = "black", xlab="grey intensity value", ylab="Percentage")
for(i in 2:n) {lines(set[i,], type=typedraw,col = "black" )}
lines(approxFG,type=typedraw, col="blue")
lines(approxF, type=typedraw,col = "green")
lines(optimalP,type=typedraw, col="red")
title(main="Jeffreys frequency centroids", sub="many randomly sampled frequency histograms" , col.main="black", font.main=3)
dev.off()
Here is the result: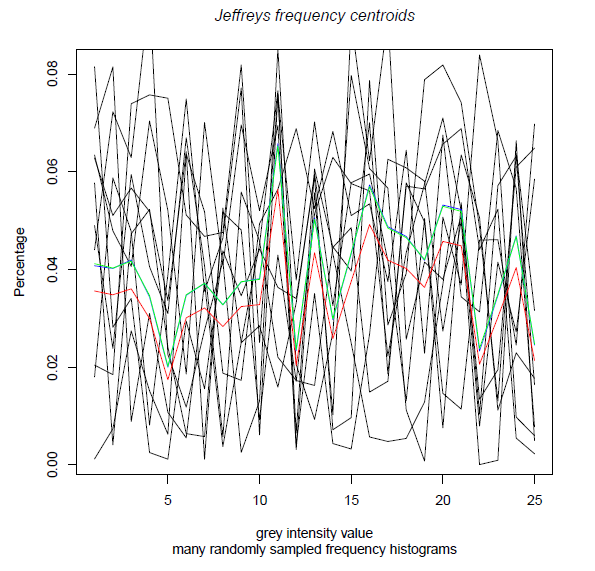
A frequency histogram may be interpreted as the parameter of a multinomial distribution (with fixed number of trials). The Kullback-Leibler divergence amounts to compute a Bregman divergence for exponential families. Therefore the Jeffreys divergence is equivalent (for exponential families) to a symmetrized Bregman divergence. Thus the SKL centroid (Jeffreys centroid) can be interpreted as a symmetrized Bregman centroid.
See:
@ARTICLE{JeffreysSKLCentroid-2013,
author={Nielsen, Frank},
journal={IEEE Signal Processing Letters},
title={Jeffreys Centroids: A Closed-Form Expression for Positive Histograms and a Guaranteed Tight Approximation for Frequency Histograms},
year={2013},
volume={20},
number={7},
pages={657-660},
doi={10.1109/LSP.2013.2260538},
ISSN={1070-9908}
}
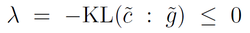
Lambda<-function(set,weight)
{
na=normalizeHistogram(ArithmeticCenter(set,weight))
ng=normalizeHistogram(GeometricCenter(set,weight))
d=length(na)
bound=rep(0,d)
for(i in 1:d) {bound[i]=na[i]+log(ng[i])}
lmin=max(bound)-1
lmax=0
while(lmax-lmin>1.0e-10)
{
lambda=(lmax+lmin)/2
cs=cumulativeCenterSum(na,ng,lambda);
if (cs>1)
{lmin=lambda} else {lmax=lambda}
}
lambda
}
JeffreysFrequencyCentroid<-function(set,weight)
{
na=normalizeHistogram(ArithmeticCenter(set,weight))
ng=normalizeHistogram(GeometricCenter(set,weight))
lambda=Lambda(set,weight)
JeffreysFrequencyCenter(na,ng,lambda)
}
KullbackLeibler<-function(p,q)
{
d=length(p)
res=0
for(i in 1:d)
{res=res+p[i]*log(p[i]/q[i])+q[i]-p[i]}
res
}
lambda=Lambda(set,weight)
ct=JeffreysFrequencyCentroid(set,weight)
na=normalizeHistogram(ArithmeticCenter(set,weight))
ng=normalizeHistogram(GeometricCenter(set,weight))
# Check that $\lambda=-\KL(\tilde{c}:\tilde{g})$
lambdap=-KullbackLeibler(ct,ng)
lambda
# difference
abs(lambdap-lambda)
We get the following console output which corroborates the lambda/KL identity:> lambda [1] -0.01237374696329113926696 > # difference > abs(lambdap-lambda) [1] 5.261388026644997495396e-11
options(digits=22)
PRECISION=.Machine$double.xmin
LambertW0<-function(z)
{
S = 0.0
for (n in 1:100)
{
Se = S * exp(S)
S1e = Se + exp(S)
if (PRECISION > abs((z-Se)/S1e)) {
break}
S = S - (Se-z) / (S1e - (S+2) * (Se-z) / (2*S+2))
}
S
}
#
# Symmetrized Kullback-Leibler divergence (same expression for positive arrays or unit arrays since the +q -p terms cancel)
# SKL divergence, symmetric Kullback-Leibler divergence, symmetrical Kullback-Leibler divergence, symmetrized KL, etc.
#
JeffreysDivergence<-function(p,q)
{
d=length(p)
res=0
for(i in 1:d)
{res=res+(p[i]-q[i])*log(p[i]/q[i])}
res
}
normalizeHistogram<-function(h)
{
d=length(h)
result=rep(0,d)
wnorm=cumsum(h)[d]
for(i in 1:d)
{result[i]=h[i]/wnorm; }
result
}
#
# Weighted arithmetic center
#
ArithmeticCenter<-function(set,weight)
{
dd=dim(set)
n=dd[1]
d=dd[2]
result=rep(0,d)
for(j in 1:d)
{
for(i in 1:n)
{result[j]=result[j]+weight[i]*set[i,j]}
}
result
}
#
# Weighted geometric center
#
GeometricCenter<-function(set,weight)
{
dd=dim(set)
n=dd[1]
d=dd[2]
result=rep(1,d)
for(j in 1:d)
{
for(i in 1:n)
{result[j]=result[j]*(set[i,j]^(weight[i]))}
}
result
}
cumulativeSum<-function(h)
{
d=length(h)
cumsum(h)[d]
}
#
# Optimal Jeffreys (positive array) centroid expressed using Lambert W0 function
#
JeffreysPositiveCentroid<-function(set,weight)
{
dd=dim(set)
d=dd[2]
result=rep(0,d)
a=ArithmeticCenter(set,weight)
g=GeometricCenter(set,weight)
for(i in 1:d)
{result[i]=a[i]/LambertW0(exp(1)*a[i]/g[i])}
result
}
#
# A 1/w approximation to the optimal Jeffreys frequency centroid (the 1/w is a very loose upper bound)
#
JeffreysFrequencyCentroidApproximation<-function(set,weight)
{
result=JeffreysPositiveCentroid(set,weight)
w=cumulativeSum(result)
result=result/w
result
}
#
# By introducing the Lagrangian function enforcing the frequency histogram constraint
#
cumulativeCenterSum<-function(na,ng,lambda)
{
d=length(na)
cumul=0
for(i in 1:d)
{cumul=cumul+(na[i]/LambertW0(exp(lambda+1)*na[i]/ng[i]))}
cumul
}
#
# Once lambda is known, we get the Jeffreys frequency cetroid
#
JeffreysFrequencyCenter<-function(na,ng,lambda)
{
d=length(na)
result=rep(0,d)
for(i in 1:d)
{result[i]=na[i]/LambertW0(exp(lambda+1)*na[i]/ng[i])}
result
}
#
# Approximating lambda up to some numerical precision for computing the Jeffreys frequency centroid
#
JeffreysFrequencyCentroid<-function(set,weight)
{
na=normalizeHistogram(ArithmeticCenter(set,weight))
ng=normalizeHistogram(GeometricCenter(set,weight))
d=length(na)
bound=rep(0,d)
for(i in 1:d) {bound[i]=na[i]+log(ng[i])}
lmin=max(bound)-1
lmax=0
while(lmax-lmin>1.0e-10)
{
lambda=(lmax+lmin)/2
cs=cumulativeCenterSum(na,ng,lambda);
if (cs>1)
{lmin=lambda} else {lmax=lambda}
}
JeffreysFrequencyCenter(na,ng,lambda)
}